数论四大定理讲解（数论中孙子定理的简单理解）

孙子定理是中国古代求解一次同余式组的方法。是数论中一个重要定理。又称中国余数定理。一元线性同余方程组问题最早可见于《孙子算经》，叫做“物不知数”问题，原文如下：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。《孙子算经》中首次提到了同余方程组问题，及以上具体问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。

这里引用百度百科中给出的证明：

用现代数学的语言来说明的话，中国剩余定理给出了以下的一元线性同余方程组：

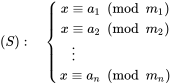
有解的判定条件，并用构造法给出了在有解情况下解的具体形式。

中国剩余定理说明：假设整数m1,m2, ... ,mn两两互质，则对任意的整数：a1,a2, ... ,an，方程组（S）有解，并且通解可以用如下方式构造得到：

假设

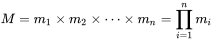
是整数m1,m2, ... ,mn的乘积，并设

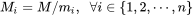
是除了mi以外的n- 1个整数的乘积。

为了理解上面的公式，这里给出一个最简单的例子：

一个整数除以2余1，除以3余2，求这个整数。

我们知道，这个数字就是5、11、17、23等等。

按照以上公式，这里m1=2,m2=3; a1=1,a2=2。

M=2x3=6，M1=3,M2=2。

为了使得M1*t1=3*t1(mod2)=1,则t1=1；

为了使得M2*t2=2*t2(mod3)=1,则t2=2。

则所求的数字为a1*M1*t1+a2*M2*t2=1*3*1+2*2*2=11,再加上kM，也就是6k，得到所有的解

5,11,17,23,29......

理解上述定理的关键就在于，对于求和式

a1*M1*t1+a2*M2*t2 来说，它必须保证被2除余1，同时又必须保证被3除余2。

当被2除的时候，a1*M1*t1保证了余数是1，因为M1*t1对于模2来说就是1，而a1本身就是模2的余数1；后半部分a2*M2*t2因为因子M2本身包含了2，因此它被2整除的时候余数就是0，两者加起来就保证了模2余1；

当被3除的时候，前半部分a1*M1*t1则保证了对于模3来说余数是0；后半部分a2*M2*t2则保证了它被3整除的时候余数是2，两者加起来就保证了模3余2。

所以a1*M1*t1+a2*M2*t2整个式子既保证了进行模2运算时余1，又保证了模3运算时余2。

总之，所求x的和式

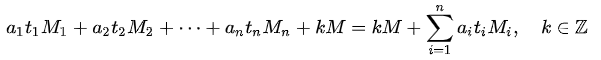
的第一项保证了被m1求余的时候余数是a1，其它项则保证了被m1求余的时候余数都是0；

第二项则保证了被m2求余时余数是a2，其它项则保证了被m2求余的时候余数也都是0；

。。。。。。

最后加上的 kM 对于任何因子 mi 的模运算其余数都是0，所以不会改变结果。

因此，x的总的和式，保证了被每一个mi求模运算的时候其余数都是ai。

下面对孙子算经中的问题给出解答。

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。

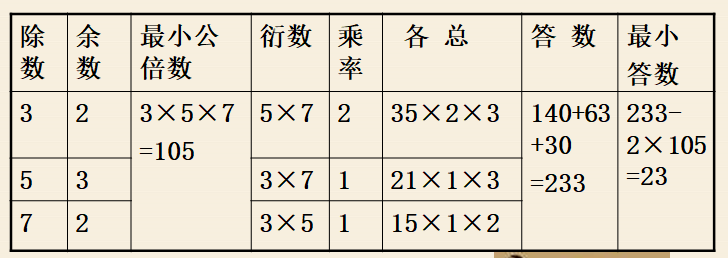
因为-1=（-1）*3+2，所以-1模3的余数和35模3的余数都是2；因为两个数模3的余数都是2，所以它们的乘积35x(-1）模3的余数就是1。

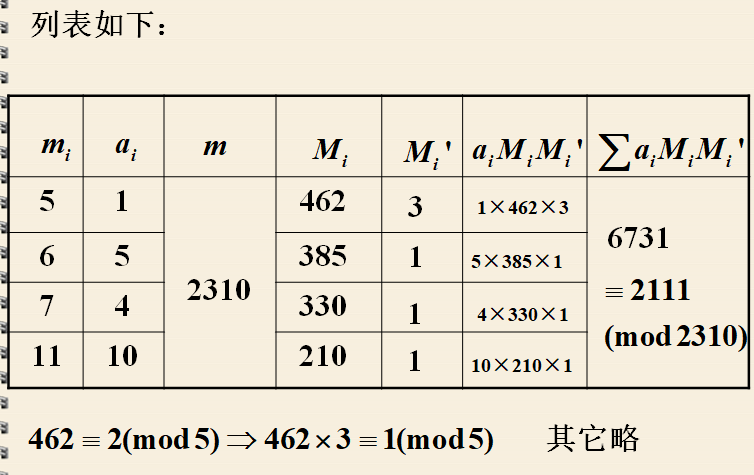
再看一个韩信点兵的问题。